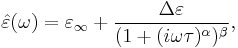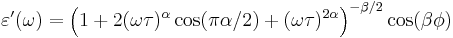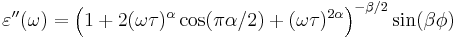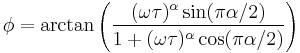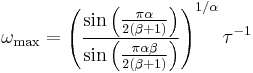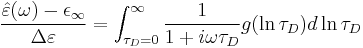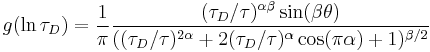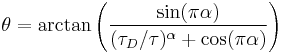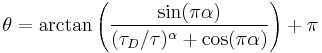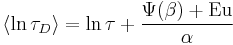Havriliak–Negami relaxation

Havriliak–Negami relaxation is an empirical modification of the Debye relaxation model, accounting for the asymmetry and broadness of the dielectric dispersion curve. The model was first used to describe the dielectric relaxation of some polymers,[1] by adding two exponential parameters to the Debye equation:

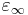\hat{\varepsilon}(\omega) = \varepsilon_{\infty} %2B \frac{\Delta\varepsilon}{(1%2B(i\omega\tau)^{\alpha})^{\beta}},

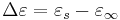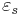where \varepsilon_{\infty} is the permittivity at the high frequency limit, \Delta\varepsilon = \varepsilon_{s}-\varepsilon_{\infty} where \varepsilon_{s} is the static, low frequency permittivity, and \tau is the characteristic relaxation time of the medium. The exponents \alpha and \beta describe the asymmetry and broadness of the corresponding spectra.

Depending on application, the Fourier transform of the stretched exponential function can be a viable alternative that has one parameter less (Occam's razor).

For 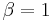\beta = 1 the Havriliak–Negami equation reduces to the Cole–Cole equation, for 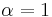\alpha=1 to the Cole–Davidson equation.

The storage part 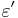\varepsilon' and the loss part 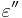\varepsilon'' of the permittivity (here: 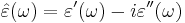\hat{\varepsilon}(\omega) = \varepsilon'(\omega) - i \varepsilon''(\omega) ) can be calculated as

\varepsilon'(\omega) = \left( 1 %2B 2 (\omega\tau)^\alpha \cos (\pi\alpha/2) %2B (\omega\tau)^{2\alpha} \right)^{-\beta/2} \cos (\beta\phi)

and

\varepsilon''(\omega) = \left( 1 %2B 2 (\omega\tau)^\alpha \cos (\pi\alpha/2) %2B (\omega\tau)^{2\alpha} \right)^{-\beta/2} \sin (\beta\phi)

with

\phi = \arctan \left( { (\omega\tau)^\alpha \sin(\pi\alpha/2) \over 1 %2B (\omega\tau)^\alpha \cos(\pi\alpha/2) } \right)

The maximum of the loss part lies at

\omega_{\rm max} = \left( { \sin \left( { \pi\alpha \over 2 ( \beta %2B1 ) } \right) \over \sin \left( { \pi\alpha\beta \over 2 ( \beta %2B1 ) } \right) } \right) ^ {1/\alpha} \tau^{-1}

The Havriliak–Negami relaxation can be expressed as a superposition of individual Debye relaxations

{ \hat{\varepsilon}(\omega) - \epsilon_\infty \over \Delta\varepsilon } = \int_{\tau_D=0}^\infty { 1 \over 1 %2B i \omega \tau_D } g( \ln \tau_D ) d \ln \tau_D

with the distribution function

g ( \ln \tau_D ) = { 1 \over \pi } { ( \tau_D / \tau )^{\alpha\beta} \sin (\beta\theta) \over ( ( \tau_D / \tau )^{2\alpha} %2B 2 ( \tau_D / \tau )^{\alpha} \cos (\pi\alpha) %2B 1 )^{\beta/2} }

where

\theta = \arctan \left( { \sin (\pi\alpha) \over ( \tau_D / \tau )^{\alpha} %2B \cos (\pi\alpha) } \right)

if the argument of the arctangent is positive, else[2]

\theta = \arctan \left( { \sin (\pi\alpha) \over ( \tau_D / \tau )^{\alpha} %2B \cos (\pi\alpha) } \right) %2B \pi

The first logarithmic moment of this distribution, the average logarithmic relaxation time is

\langle \ln\tau_D \rangle = \ln\tau %2B { \Psi(\beta) %2B {\rm Eu} \over \alpha }

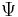where \Psi is the digamma function and 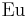{\rm Eu} the Euler constant.[3]

References

  1. ^ Havriliak, S.; Negami, S. (1967). "A complex plane representation of dielectric and mechanical relaxation processes in some polymers". Polymer 8: 161–210. doi:10.1016/0032-3861(67)90021-3. 
  2. ^ Zorn, R. (1999). "Applicability of Distribution Functions for the Havriliak–Negami Spectral Function". Journal of Polymer Science Part B 37 (10): 1043–1044. Bibcode 1999JPoSB..37.1043Z. doi:10.1002/(SICI)1099-0488(19990515)37:10<1043::AID-POLB9>3.3.CO;2-8. 
  3. ^ Zorn, R. (2002). "Logarithmic moments of relaxation time distributions". Journal of Chemical Physics 116 (8): 3204–3209. Bibcode 2002JChPh.116.3204Z. doi:10.1063/1.1446035. 

See also